Evaluating Expressions Involving Fractions
This short note is intended to remind you of principles
already described under the heading “Order of
Operations,” and to illustrate their application to
arithmetic expressions involving fractions.
In evaluating an arithmetic expression, the order in which
operations are done is:
(1) bracketed expressions first, starting with the innermost
pair of brackets
(2) powers second
(3) multiplications and divisions third
(4) additions and subtractions last Within each priority
level, operations are done from left to right.
These rules apply to all arithmetic expressions, including
those which involve fractions.
Example:
Simplify 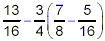
solution:
The expression in brackets gets evaluated first:
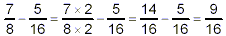
thus
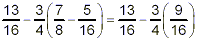
Now, the multiplication in the second term gets done, because
it has a higher priority than the subtraction:
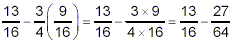
Finally, we do the subtraction:
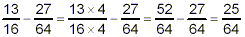
Thus, our final answer is
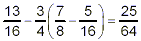
A common error is to start by doing the subtraction:
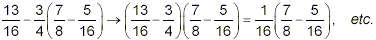
This is an error, because it carries out the subtraction ahead
of the higher priority brackets and multiplication. If carried to
completion this will give an incorrect final answer.
Example:
Simplify 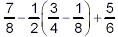
solution:
The expression in brackets has the highest priority, so do it
first:
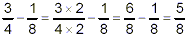
So, the original expression becomes
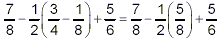
Of the remaining operations, the multiplication has the
highest priority, so do it next:
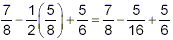
Now, we’re left with subtraction and addition. Both of
these operations have the same priority, so we work from left to
right. First, subtract 5 / 16 from 7 / 8 :
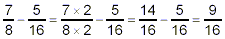
so that
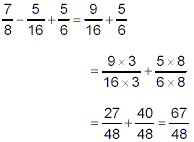
Since 67 is a prime number, this fraction cannot be simplified
further, so the final answer here is
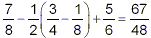
Note that if the addition and subtraction were done in the
reverse order (thus violating the priority rules), we would get
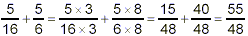
and then
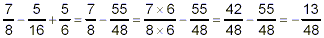
which is very different from the correct answer. So, to get
the correct answer, the conventional priority rules must be
followed very carefully.
|