The Cartesian Plane

An ordered pair (x, y) of real numbers has x as its first member and y as its second member. The model for representing ordered pairs is called the rectangular coordinate system, or the Cartesian plane, after the French mathematician René Descartes. It is developed by considering two real lines intersecting at right angles (see the figure below).

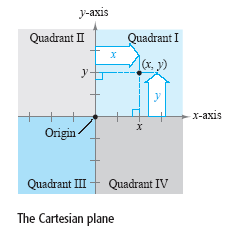
The horizontal real line is usually called the x-axis, and the vertical real line is usually called the y-axis. Their point of intersection is the origin. The two axes divide the plane into four quadrants.

Each point in the plane (x, y) is identified by an ordered pair of real numbers x and y, called coordinates of the point. The number x represents the directed distance from the y-axis to the point, and the number y represents the directed distance from the x-axis to the point. For the point (x, y), the first coordinate is the x-coordinate or abscissa, and the second coordinate is the y-coordinate or ordinate. For example, the figure below shows the locations of the points (-1, 2), (3, 4), (0, 0), (3, 0) and (-2, -3) in the Cartesian plane.

NOTE The signs of the coordinates of a point determine the quadrant in which the point lies. For instance, if x > 0 and y < 0, then (x, y) lies in Quadrant IV.

Note that an ordered pair (a, b) is used to denote either a point in the plane or an open interval on the real line. This, however, should not be confusing—the nature of the problem should clarify whether a point in the plane or an open interval is being discussed.