Angles and Degree Measure
An angle has three parts: an initial ray, a terminal ray, and a
vertex (the point of
intersection of the two rays), as shown in the figure below.
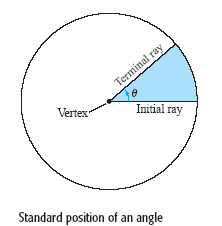
An angle is in standard position
if its initial ray coincides with the positive x-axis and its vertex is at the origin.
We assume that you are familiar with the degree measure of an angle. It is common
practice to use θ (the Greek lowercase theta) to represent both an angle and its
measure. Angles between 0º and 90º are acute, and angles between 90º and
180º are
obtuse.
Positive angles are measured counterclockwise, and negative angles are measured
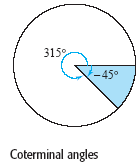
clockwise. For instance, the figure below shows an angle whose measure is -45º. You
cannot assign a measure to an angle by simply knowing where its initial and terminal
rays are located. To measure an angle, you must also know how the terminal ray was
revolved. For example, this figure shows that the angle measuring -45º has the
same terminal ray as the angle measuring 315º. Such angles are coterminal. In
general, if θ is any angle, then
θ + n(360º), n is a nonzero integer
is coterminal with θ.
An angle that is larger than 360º is one whose terminal ray has been revolved
more than one full revolution counterclockwise, as shown in the following
figure.
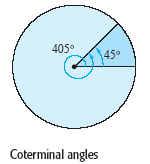
NOTE
It is common to use the simbol θ to refer to
both an angle and its measure. For instance, in the previous figure, you can
write the measure of the smaller angle as θ = 45º.
Radian Measure
To assign a radian measure to an angle θ, consider
θ to be a central angle of a circle
of radius 1, as shown in the figure below.
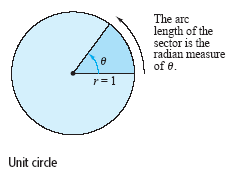
The radian measure of θ is then defined to be
the length of the arc of the sector. Because the circumference of a circle is 2πr,
the
circumference of a unit circle (of radius 1) is 2π.
This implies that the radian
measure of an angle measuring is 360º. In other words, 360º = 2π radians.
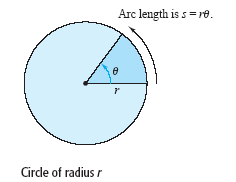
Using radian measure for θ, the length s of a circular arc of radius r is
s = rθ, as
shown in the figure below.
You should know the conversions of the common angles shown in the next
figure. For other angles, use the fact that is equal to radians.

|