Completing the Square
Any quadratic equation can be solved using a technique called completing the square.
To use this method, we will rewrite the quadratic equation so that one side
is a perfect square. Then we solve using the square root property.
Before we solve a quadratic equation in this way, let’s learn how to
complete the square.
To “complete the square†means to transform a binomial of the form
x2 + bx into a perfect square trinomial by adding a constant term.
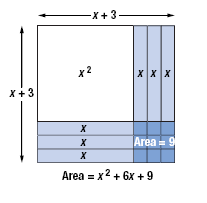
For example, let’s complete the square for x2 + 6x.
We will use rectangles, called algebra tiles, to visualize the process.
• A square tile measuring x units on a side has area x2. We will use this
tile to represent x2, the first term of x2 + 6x.
• A rectangular tile that is x units tall and 1 unit wide has an area of 1x.
Since 6 · 1x is 6x, we will use six of these tiles to represent the second
term of x2 + 6x.
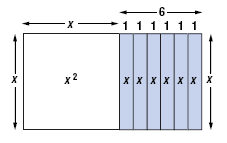
Placed side by side, the tiles form a rectangle that represents x2
+ 6x.
Now, we try to rearrange the tiles to form a square.
To do this, we move one-half of the tall thin tiles.
However, the result is not a complete square because the lower right
portion is missing.
The missing piece is a 3-by-3 square.
Thus, to “complete the square,†we must add 3 · 3
= 9 unit tiles.
With the 9 new tiles, the area of the entire square is
(x + 3)(x + 3) = (x + 3)2 = x2 + 6x + 9.
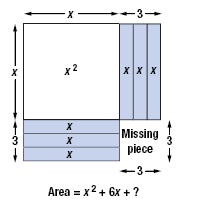
By adding 9 to x2 + 6x, we have created the perfect square (x + 3)2.
| Let’s review the process we used to
complete the square.
We moved one-half of the x-tiles. |
x2 + 6x + ?
Multiply the coefficient of x by
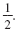
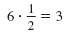
|
| Then we filled in the remaining
space with a square of unit tiles. |
Square the result.
32 = 9 |
| We added nine tiles to complete the
square. |
x2 + 6x + 9
= (x + 3)(x + 3)
= (x + 3)2 |
 This process holds in general:
To find the number needed to complete the square, multiply the coefficient
of the x-term by
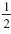 , and then square the result. , and then square the result.
|