Composition of Functions
Another way to combine two functions is called the composition of
functions. This is where the output of one function becomes the input of a
second function.
Definition—
Composition of Functions
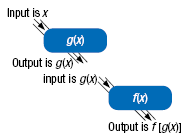
Let f(x) and g(x) represent two functions. The composition of f and
g, written (f ○ g)(x), is defined as
(f ○ g)(x) = f[g(x)]
Here, g(x) must be in the domain of f(x). If it is not, then f[g(x)] will
be undefined.
Note:
In the composition (f ○ g)(x), the output
from g(x) is the input for f(x).
Example 1
Given f(x) = 3x - 5 and g(x) = x2 - 7, find:
a. (f ○ g)(x)
b. (g ○ f)(x)
Solution
| a. |
Use g(x) as the input for f(x).
Replace g(x) with x2 - 7.
In f(x), replace x with x2 - 7.
Remove parentheses.
Subtract.
So, (f ○ g) = 3x2
- 26. |
(f ○
g)(x) |
= f[g(x)] = f[x2 - 7]
= 3(x2 - 7) - 5
= 3x2 - 21 - 5
= 3x2 - 26 |
| b. |
Use f(x) as the input for g(x).
Replace f(x) with 3x - 5.
In g(x), replace x with 3x - 5.
Square the binomial.
Combine like terms. |
(g ○ f)(x) |
= g[f(x)]
= g[3x - 5]
= (3x - 5)2 - 7
= 9x2 - 15x - 15x + 25 - 7
= 9x2 - 30x + 18 |
So, (g ○ f)(x) = 9x2 - 30x
+ 18.
Notes:
In (f ○ g)(x) = f[g(x)], we substitute the
expression for g(x) into f(x).
In (g ○ f)(x) = g[f(x)], we substitute the
expression for f(x) into g(x).
In this example:(f ○ g)(x) = 3x2
- 19
(g ○ f)(x) = 9x2 - 30x + 18.
In most cases, (f ○ g)(x) and (g ○ f)(x) do NOT yield the same result.
|