Methods for Solving Quadratic Equations
Quadratic equations are of the form ax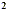 + bx + c = 0, where a + bx + c = 0, where a 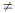 0 0
Quadratics may have two, one, or zero real solutions .
1. Completing the Square
If the quadratic equation is of the form ax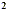 + bx + c = 0, where a + bx + c = 0, where a 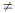 0 and the quadratic expression is not factorable,
try completing the square. 0 and the quadratic expression is not factorable,
try completing the square.
Example: x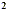 + 6x - 11 = 0 + 6x - 11 = 0
**Important: If a 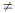 1, divide all terms by “a” before
proceeding to the next steps. 1, divide all terms by “a” before
proceeding to the next steps.
2. Quadratic Formula
Any quadratic equation of the form ax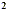 + bx + c = 0, where a + bx + c = 0, where a 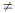 0 can be solved for both real and imaginary
solutions using the quadratic formula: 0 can be solved for both real and imaginary
solutions using the quadratic formula:
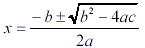
Example: x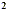 + 6x - 11 = 0 (a = 1, b = 6, c = -11) + 6x - 11 = 0 (a = 1, b = 6, c = -11)
Substitute values into the quadratic formula:
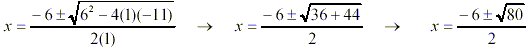 Simplify the radical Simplify the radical
 This is the final simplified EXACT
answer. This is the final simplified EXACT
answer.
|