Properties of Common Logs

Name	Property	Example
Log of a Product	log uv = log u + log v	log 5x = log 5 + log x
Log of a Quotient
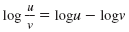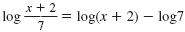Log of a Power	log un = n · log u	log 42 = 2 · log 4
	10 log u = u	10 log 7 = 7

Here are three special cases involving common logs:

• log1 = log₁₀ 1 = 0 because 10⁰ = 1.

• log10 = log₁₀ 10 = 1 because 10¹ = 10.

• log10ⁿ = log₁₀ 10ⁿ = n because log10ⁿ = n · log 10 = n · 1 = n.

Example 1

Write 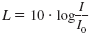as an equation containing two logs.

Solution

The right side contains the log of quotient.
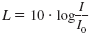Use the Log of Quotient Property.	L = 10 · (log I - log I0)

So 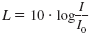can be written as L = 10 · (log I - log I₀).

Note:

Notice that logI - logI₀ must be in parentheses since 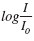was multiplied by 10.