Properties of Exponents
Exponential notation is a shorthand way of writing repeated
multiplication of the same number.
For example, 53 is a shorthand way of writing 5
· 5 · 5.
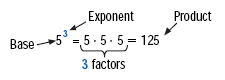
In the expression 53:
• The base, 5, is the repeated factor.
• The exponent, 3, is the number of times the base appears as a factor.
An exponent is also called a power.
An exponent is not always a positive real number. Here is the definition of
a negative exponent:
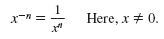
Using this definition, we can show that:

Example 1
Write without using a negative exponent and then simplify: 6-3
Solution
Note
The sign of the exponent does not indicate
the sign of the number.
For example, 6-3 has a negative exponent,
-3. But it simplifies to a positive number.
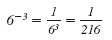
As another example, -32 has a positive exponent. But it simplifies to a negative
number:
-32= -3 · 3 = -9
Example 2
Write without using a negative exponent: 8wy-2.Solution
|