Solving Quadratic Equations by Using the Quadratic Formula
Objective Introduce the Quadratic Formula and
learn how to use it to solve quadratic equations.
In this lesson, you will use the Quadratic Formula to solve
quadratic equations. The goal is that you become comfortable
using this formula. This will require lots of practice, and so
you should pay special attention to the examples.
The Quadratic Formula The solutions of a
quadratic equation in the form ax 2 + bx + c = 0,
where a 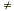 0, are given by the formula 0, are given by the formula 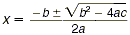 . .
This formula can be used to find the solutions to any
quadratic equation.
Notice the 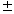 sign in the formula. This means that
there may be two solutions to a quadratic equation. Recall that a
parabola intersects the x -axis in two places, the corresponding
equation has two solutions. This corresponds to the two solutions sign in the formula. This means that
there may be two solutions to a quadratic equation. Recall that a
parabola intersects the x -axis in two places, the corresponding
equation has two solutions. This corresponds to the two solutions
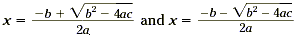 . .
The expression inside of the square root, b 2 -
4ac, is called the discriminant. When the
discriminant is positive, there are two distinct solutions. When
this expression is zero, the square root in the Quadratic Formula
is zero, and then there is only one solution, 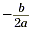 . This corresponds to
the parabola intersecting the x -axis in only one point, namely
the vertex. The final case is when the discriminant b 2
- 4ac is negative, in which case the square root . This corresponds to
the parabola intersecting the x -axis in only one point, namely
the vertex. The final case is when the discriminant b 2
- 4ac is negative, in which case the square root 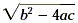 is not defined. In this
case, there are no real solutions to the quadratic equation. This
corresponds to the parabola not intersecting the x-axis at all. is not defined. In this
case, there are no real solutions to the quadratic equation. This
corresponds to the parabola not intersecting the x-axis at all.
| Solutions
of the Quadratic Equation ax 2
+ bx + c = 0 |
| Discriminant |
b 2 - 4ac >
0 |
b 2 - 4ac = 0 |
b 2 - 4ac <
0 |
| Number of Solutions |
2
|
1
|
0
|
| Example |
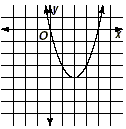
|
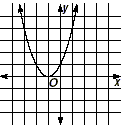
|
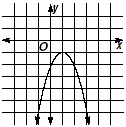
|
| Parabola Intersects the x-axis |
yes, in two distinct
points |
yes, in exactly one point,
the vertex |
no |
|