Solving Absolute Value Inequalities
Solving an Absolute Value Inequality of the
Form | x| > a
Principle
Absolute Value Inequalities of the Form | x| > a and | x| ≥ a
Let a represent a positive real number.
| • If |x| > a, then x < -a or x > a. |
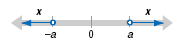 |
| • If |x| ≥ a, then x
≤ -a or x ≥ a. |
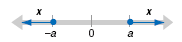 |
• If |x| > 0, then the solution is all real numbers, except 0.
• If |x| ≥ 0, then the solution is all real numbers.
• If |x| > -a, then the solution is all real numbers.
• If |x| ≥ -a, then the solution is all real numbers.
Note:
The absolute value of a number or expression is always
greater than a negative number.
Next, let’s solve some absolute value inequalities of the form |x| > a and
x| ≥ a.
Example 1
Solve: 3|5x| ≥ 60.
| Solution
Step 1 Isolate the absolute value.
Divide both sides by 3.
Step 2 Make the substitution w = 5x.
Step 3 Use the Absolute Value
Principle to solve for w.
Step 4 Replace w with 5x.
Step 5 Solve for x.
Divide each side by 5. |
3|5x|
≥ 60
|5x| ≥ 20
|w| ≥ 20
w ≤ -20 or w ≥ 20
5x ≤ -20 or 5x ≥ 20
x ≤ -4 or x ≥ 4 |
| |
|
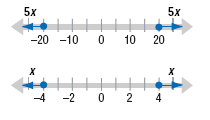
Step 6 Check the answer.
There are infinitely many solutions. It is a good idea to check one
number from each part of the solution. Let’s check x = -6 and
x = 7.
| Check x = -6 |
Check x = 7 |
| Is
Is
Is
Is |
3|5x| ≥
3|5(-6)| ≥
3|-30| ≥
3 · 30 ≥
90 ≥ |
60 60 ?
60 ?
60 ?
60 ? Yes |
Is
Is
Is
Is |
3|5x| ≥
3|5(7)| ≥
3|35| ≥
3 · 35 ≥
105 ≥ |
60 60 ?
60 ?
60 ?
60 ? Yes |
So, the solution is x ≤ -4 or x
≥ 4.
Note:
You may be tempted to write x ≤ -4 or x
≥ 4
as
-4
≥ x
≥ 4.
However, this implies that -4 is greater
than 4, which is false.
We cannot write x ≤ -4 or x
≥ 4 as a
single compound inequality.
|